dessn.investigations.zeropoints package

A fully rigorous analysis would be expected to integrate zero point uncertainty and covariance by having the conversion between counts and flux. However, this is numerically infeasible, as there are so many observational effects that must be included to get the actual flux and flux error. Because of this, zero point uncertainty is generally propagated into analysis by determining the numerical derivative of the parameters of interest (generally apparent magnitude, stretch and colour of the supernovae) with respect to the zero points by simulations. In doing this, there is an assumption made about the linearity of the gradient surface. For our DES-like data sample, we find that numerical derivatives remain linear on scales exceeding \(5\sigma\), and so utilise this method like previous analyses.

As normal, we take a base light curve, and then - for each band we have - we shift the flux and flux error for those observations lke we had perturbed the zero point, and compare the difference in SALT2 fit summary statistics between the base light curve and the perturbed light curve.

With typical zero point uncertainty estimated to be of the order of \(0.01\) mag, we calculate numerical derivatives using that \(\delta Z_b = 0.01\). Identical results were used found when using \(\delta Z_b = 0.05\) and when using either Newton’s difference quotient or symmetric difference quotient.

Using several thousand supernova and simulating an underlying population which has dispersion in magnitude, stretch and colour, we produce the following plot.

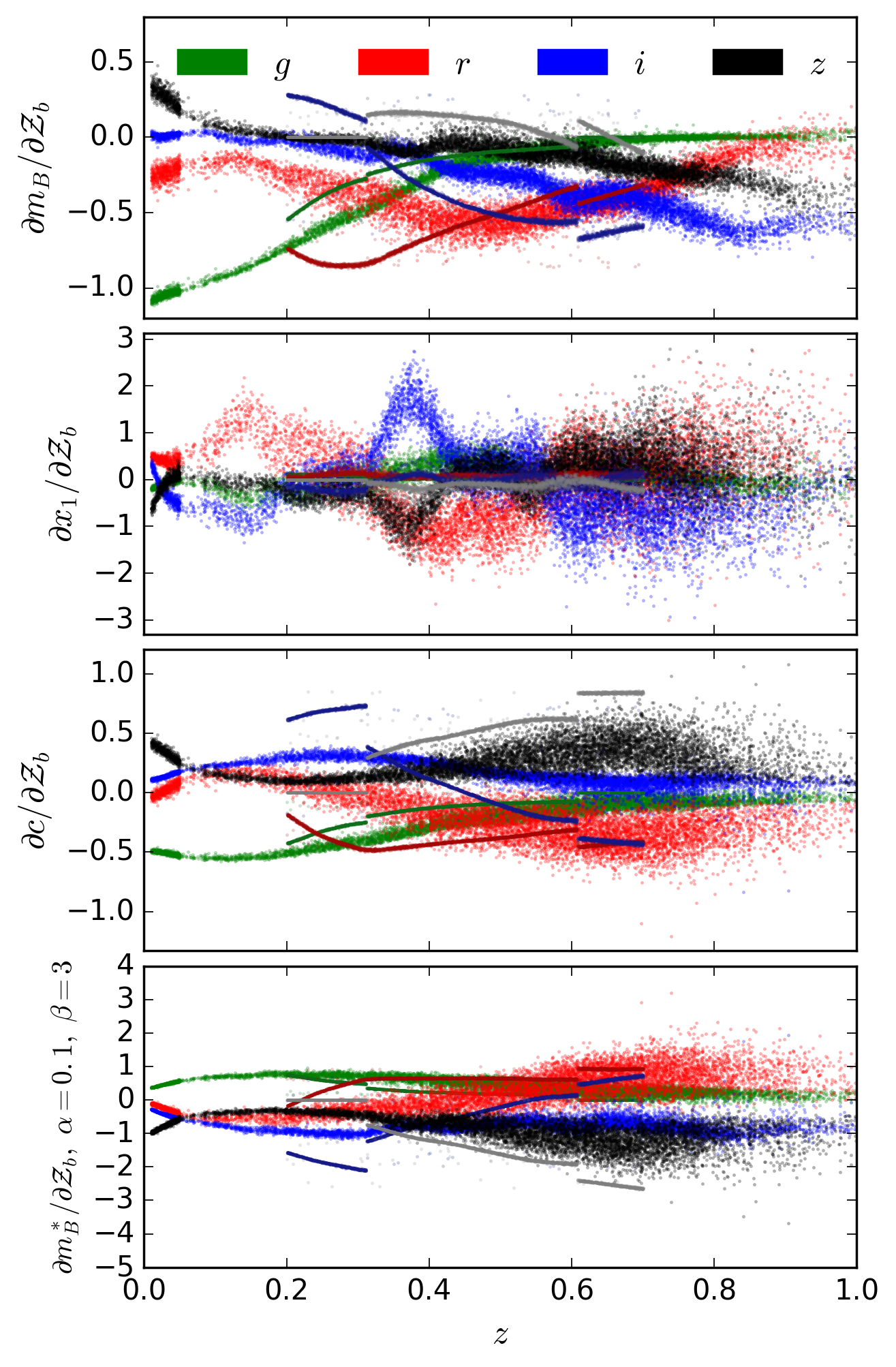
The lighter and more disperse colours show the numerical gradients I have calculated. The darker, tighter and discontinuous lines are gradients Chris Lidman has calculated (using canonical supernova). Whilst he is using DES observations and I assume fixed cadence, the disparity between the curves is a concern and needs to be figured out. I should note that the underlying population I draw from is not the issue here - I still have many times his dispersion when I collapse my underlying supernova population into a delta function.